1. 선형 회귀란?
아래와 같이 X를 입력하면 Y값이 나오는 시스템이 있다고 가정하자.
X : [ 2015, 2016, 2017]
Y : [ 2020, 2021, 2022]
우리는 직관적으로 보면 5가 더해진다고 생각이 가능하고, Y = X + 5라고 알 수 있다.
하지만, 데이터가 많아지고 식이 더 복잡해지면 사람의 두뇌로는 불가능하다.
그래서 우리는 컴퓨터에게 이런 문제를 대신 시켜야 한다.
그러면 컴퓨터는 어떻게 X + 5 라는 식을 유추해낼 수 있을까?
바로 선형회귀를 사용해서 풀 수 있다.
이걸 가능하게 하려면 먼저 가설을 세워야 한다.
간단하게 가설을 아래처럼 세워 보도록 하자.
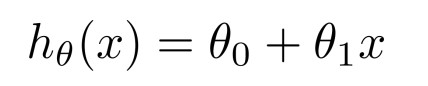
이때, 앞의 예제랑 비교하면 θ1은 1, θ0은 5이다.
우리 컴퓨터는 이 θ들을 '어떻게든' 찾아내는게 목표다.
제일 처음 가설을 초기화 할 때 우리는 임의의 값을 넣어 줄 수 있다. 왜냐면 어떤 값인지 모르니까.
대충 θ0= 1, θ1 = 0 이런식으로 넣을거고 이 θ들을 정답에 가깝게 만들어야 한다.
이렇게 학습하려면 현재 θ들이 얼마나 잘못되었나를 비교할 척도가 필요한데, 그 척도를 Cost라고 한다.
이 Cost를 앞으로 함수형태로 표현할건데, 이 Cost Function을 J라고 한다.
따라서, J(θ0,θ1)라고 하면 현재 θ들이 얼마나 잘못되었는지 나타내는 함수이다.
2. Cost Function
Cost Function은 '얼마나 잘못되었는가'를 나타내는 척도이다.
우리는 지금, 이 회귀문제를 풀건데 그러기 위해 최소제곱법을 사용한다.
목표가 되는 데이터들이 있을거고, 우리는 이 가설 h = θ0 + θ1x를 최대한 목표에 가깝게 조절할것이다.
최소제곱법은 지금 우리 가설과 목표가되는 점들이 얼마나 차이나는가를 보여주는 방법이다.
간단하게, 각 데이터로부터 얼마나 차이나는지를 계산을 할건데, 각 데이터와 가설이 되는 점들의 차를 제곱해서 전부 더한 뒤, 데이터의 개수로 나눠준다.
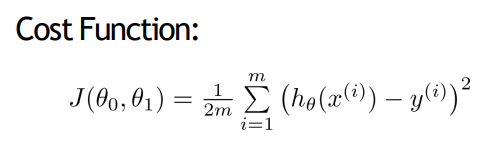
즉, 이 Cost Function의 값이 크다는것은 오류가 크다는 소리이고, 그래서 이 J(θ0,θ1)를 잘 조절해서, 비용이 줄어들 수 있도록 하는게 목표이다.
그럼 이걸 어떻게 줄일 수 있을까?
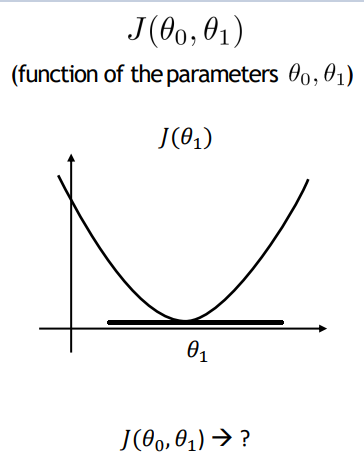
먼저 아래 사진처럼 θ1에 대해서만 생각해보자, θ1은 우리 가설에서 기울기에 해당한다.
J(θ1)이 최소가 되는 지점은 기울기가 0이되는 지점일거고, 우리는 이 기울기를 이용해서 최소가 되는 지점을 찾을 것이다.
3. Gradient descent
자, 우리는 근데, 임의의 지점을 쓸거고, 처음 값이 최소가 되는 지점일 확률은 극히 낮다.
그래서 우리는 아래 사진처럼 계속 업데이트 시켜주는데,
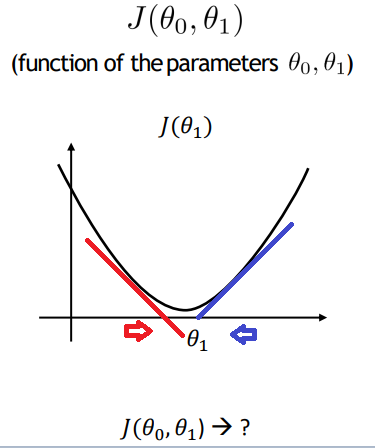
즉, 기울기가 음수라면 오른쪽으로, 기울기가 양수라면 왼쪽으로 보내줄것이다.
가장 최적의 θ1을 찾으려면 반복적으로 기울기를 계속 구해서 증감을 시킨다음, Global Optimum에 도달하게 할 수 있다.
이런 방법을 경사 하강법이라고 한다.
이걸 수식으로 나타내면 아래 사진처럼 된다.
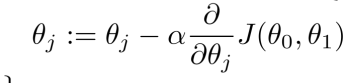
즉, Cost를 줄이기 위해 반복적으로 기울기를 계산하여 변수의 값을 변경해나가는 과정을 말한다,
그러면 θ0에 대해서는 어떻게 될까?
똑같은 과정이 들어간다.
θ0과 θ1을 따로따로 계산해서 변경시켜서 최적의 θ0, θ1을 찾을 것이다.
이때 기울기를 계산하기 위해 미분법이 필요하다.
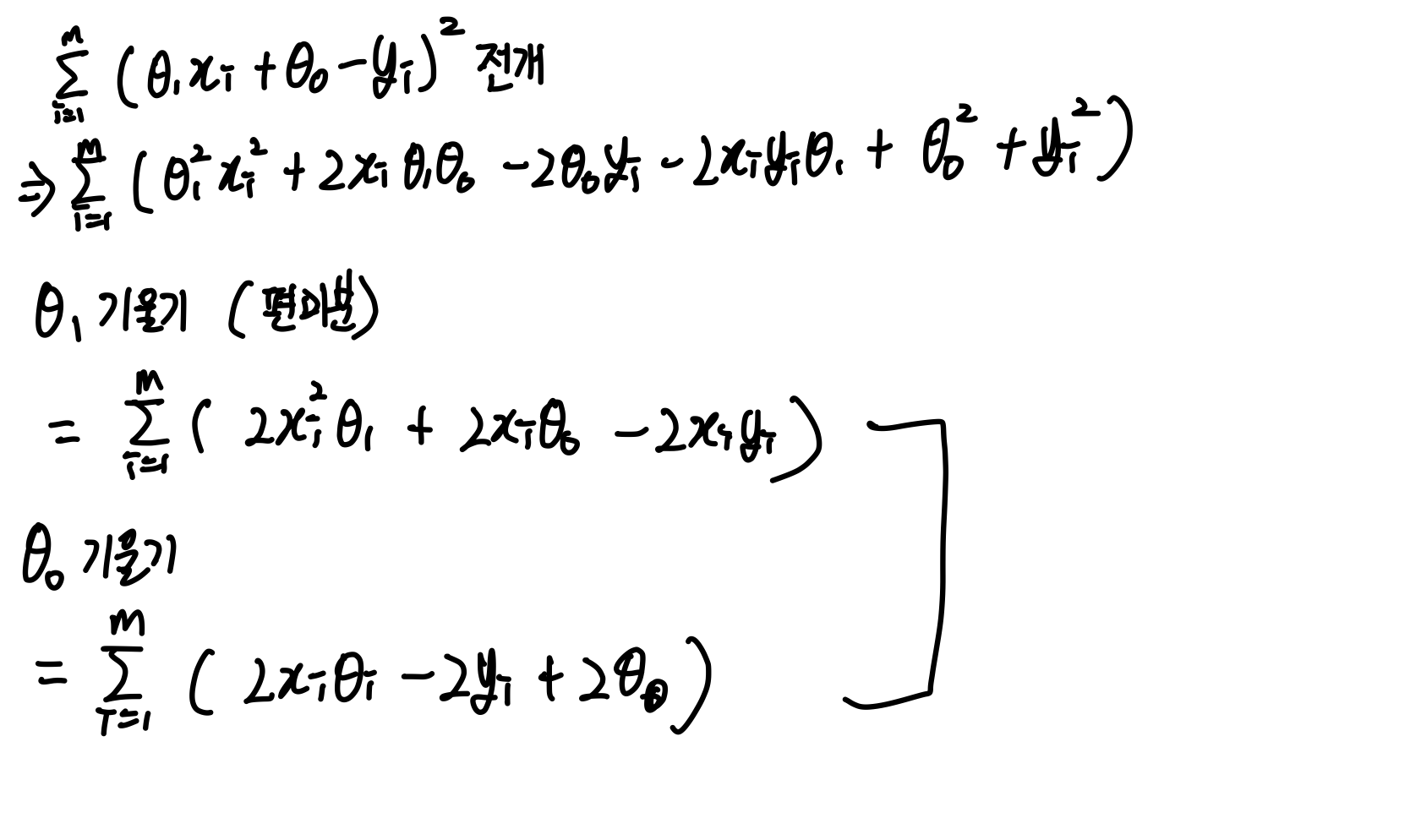
편미분으로 이런식으로 계산이 가능하다. 이제 컴퓨터는 사이클을 돌거야.가설 h(θ0, θ1)을 설정하고, 해당하는 j(θ0, θ1)을 구해서 0인지 아닌지 판단을 한 뒤, 만약 0이라면 그대로 시스템이 종료되는거고0이 아니라면 0을 향해 찾아간다.
찾아가는 과정은 당연히 θ0과 θ1을 업데이트 해주는 것이고, 이렇게 반복되는 과정을 Epoch라고 한다. epochㄷ
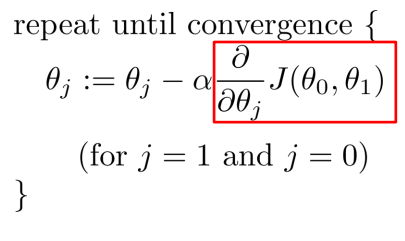
'학교 수업 > 기계학습' 카테고리의 다른 글
| 4. Linear Regression with multiple variables (3) Normal equation (0) | 2021.10.18 |
|---|---|
| 3. Linear Regression multiple variable (2) - gradient descent (0) | 2021.10.17 |
| 2. Linear Regression with multiple variable (1) (0) | 2021.10.17 |



댓글