1. Feature Scaling
다수의 feature가 있을때에 Linear Regression이 어떻게 적용되는지 지난 포스팅에서 다뤘다.
여기서는 Gradient descent를 어떻게 잘 활용할 수 있을지 알아 볼 것이다.
Feature scaling이란 먼저, 각각의 피쳐들을 비슷한 스케일로 변형시키는 것이다.
이것이 왜 필요한 지 직관적으로 그래프로 살펴보도록 하자.
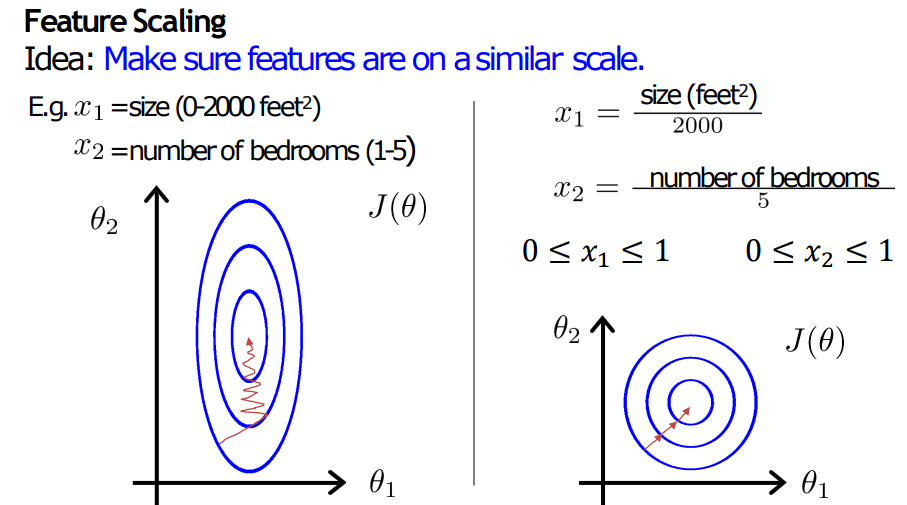
왼쪽의 그래프는 Feature Scaling 전이고 오른쪽은 후이다.
왼쪽은 피쳐들의 크기가 차이가 많이 나서 Gradient descent를 하는 cost function의 그래프가 타원형으로 찌그러져서 만들어지게 된다.
즉, 오른쪽 그래프 보다 더 많은 Gradient descent를 해야만 Global optima를 찾을 수 있다.
Feature Scaling의 한가지 방법으로 Mean normalization이 있다.

간단하게 보면 바로 이해 될 것이다.
2. Learning Rate
우리는 J(θ)의 값을 최소화시키는 θ를 반복해서 기울기를 빼주면서 찾는것이 목적이다.
이때, 정상적이라면 아래 그래프처럼 반복 횟수에 따라서 J(θ)값이 점점 줄어들 것이다.

기울기를 빼 줄때, 앞에 있는 alpha값이 중요한데,
그 alpha값을 어떻게 설정하냐에 따라 그래프가 바뀌게된다.

alpha가 너무 클 경우, 수렴을 하지 않고 발산을 해 버린다거나, 반복된다거나 할 수 있다.
따라서, 적당한 alpha 값을 찾는것이 중요하다.

문제를 통해 살펴보자.
alpha값이 너무 클 경우 수렴하지 않고 발산할 수도 있다고 했다. 따라서 C의 값이 가장 크게 될 것이다.
그러면 A와 B는 어떻게 구분할까?
alpha가 작은 경우라고 생각해보자, θ를 업데이트하는 과정에서 alpha의 값이 작다면 천천히 수렴하게 될 것이고 alpha값이 적당히 크다면 급격하게 수렴하게 될 것이다.
그래프를 보면 A가 급격하게 수렴했다는 것을 살펴 볼 수 있다.
따라서 C > A > B의 형태인 2번이 정답인 것을 유추 할 수 있다.
'학교 수업 > 기계학습' 카테고리의 다른 글
| 4. Linear Regression with multiple variables (3) Normal equation (0) | 2021.10.18 |
|---|---|
| 2. Linear Regression with multiple variable (1) (0) | 2021.10.17 |
| 1. 선형 회귀 ( Linear Regression) (0) | 2021.09.08 |



댓글